Peter Kennedy passed away suddenly on August 30, after a bicycle ride and swim near his Whistler home.
He was the best teacher. His ability to remember students' names was legendary. He did it by association "I remembered your name was Peter because you have a red coat, and my hair is red and my name is Peter" (which worked until Peter didn't bring his red coat to class one day).
He had a special ability to make things clear. I remember one day dropping by his office and talking about some problem that was worrying me. I don't remember what he said, only the feeling of mental clarity afterwards- my mind was at peace. He made everything seem simple and straightforward.
He shared that ability with the academic world through the bestselling book A Guide to Econometrics, dedicated "to Anna and Red who, until they discovered what an econometrician was, were very impressed that their son might become one."
The first editions of A Guide explained econometrics with minimal use of equations and formal notations. Regression analysis was explained with "the ballentine", inspired by the label of an Australian beer of that name.

Y is what the regression is trying to explain – for example, the variation in students' test scores, why some students get high grades and some students get low grades. X is an explanatory variable, for example, the time spent studying. What a regression analysis does is figure out how much of the variation in Y is explained by the variation in X – that is, how big the purple area is. If the purple area is large, X explains most of the variation in Y, if it is small, X does not explain much.
The picture looks more like the beer bottle label with two explanatory variables: 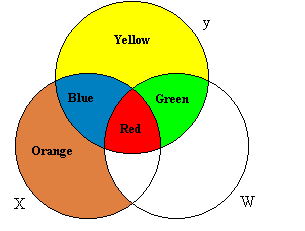
In his words:
I begin by carefully explaining the interpretations of the areas in Figure 1 as described above. Following this I put up Figure 2 on the overhead and ask the class what will happen using OLS when there is more than one explanatory variable, drawing to their attention that it is not obvious what role is played by the red area. I note that if we were to regress y on X alone, OLS would use the information in the blue plus red areas to create its estimate of bx, and if we were to regress y on W alone OLS would use the information in the green plus red areas to create its estimate of bw. I present three options for the OLS estimator when y is regressed on X and W together.
- Continue to use blue plus red to estimate bx and green plus red to estimate bw.
- Throw away the red area and just use blue to estimate bx and green to estimate bw
- Divide the red information into two parts in some way, and use blue plus part of red to estimate bx and green plus the other part of red to estimate bw.
I point out that several special cases of option c are possible, such as using blue and all of red to estimate bx and only green to estimate bw, or dividing red "equally" in some way.
After setting this up I inform students that they are to guess what OLS does, and ask them to vote for one of these options. (Voting has to be done one by one, because if the class at large is asked to vote, invariably nobody votes for anything; Kennedy (1978) is an exposition of this pedagogical device.) I have never had a majority vote for the correct answer. Next I ask the class why it would make sense for an estimating procedure to throw away the information in the red area. (It is this throwing away of the red area that allows this application of the Venn diagram to avoid being compromised by the presence of a suppressor variable.) The ensuing discussion is quite useful, with good students eventually figuring out the following.
The information in the red area is bad information – it has y "moving together" with X and also with W so that we don’t know if the movements in y are due to X or due to W, so to be on the safe side we should throw away this information.
If only the blue area information is used to estimate bx and the green area information is used to estimate bw, unbiased estimates are produced, because the blue area corresponds to variation in y uniquely attributable to X and the green area corresponds to variation in y uniquely attributable to W.
An instructor may wish to elaborate on point b by noting that the variation in y in the red area is actually due to joint movements in X and W because the red area corresponds to X and W “moving together” as well as to y and X moving together and y and W moving together. Suppose that in the red area when X changes by one W changes by two, so that a joint movement of one by X and two by W gives rise to a movement in y of bx + 2bw. If bx = 5 and bw= 7, this would be a movement of 19. If we were to match this 19 movement in y with a unit movement in X we would get a bx estimate badly off the true value of bx = 5. When this is combined with the unbiased estimate coming from the blue area information, a biased estimate results. Similarly, if the 19 movement in y were matched with a two movement in W we would get an estimate of 9.5 for bw, badly off its true value of 7.
Peter Kennedy is survived by his wife Nancy, "his companion and best friend of 40 years."
This is very sad news. I only met Peter a couple of times, but his contributions to econometrics – and especially the teaching of econometrics – were huge.
The only econometrics book I’ve ever bought that I didn’t have to buy.
This is very sad news. I actually wrote him a “fan letter” by e-mail several years ago to express how valuable his textbook had been for me as a student. Not only did he send me a very friendly thank-you e-mail, but he pleasantly surprised me by sending me drafts of two new chapters from the (then) forthcoming fifth edition!
It was so sudden, too, and so unexpected given how fit and active he was. Particulates from the forest fires? The shock of swimming in cold water?
This is from the SFU web page: A ceremony celebrating Peter’s life will take place on Friday September 17th, 10:30am at the SFU Burnaby Mountain Diamond Alumni Center.
For those of you who cannot attend, messages about Peter can be sent to pkennedy-memorial@sfu.ca
His death notice in the newspaper requested donations in Peter Kennedy’s memory be made to the Nature Conservancy of Canada.
I had the good fortune of having Peter as my instructor for an advanced undergraduate econometrics class. He was, by far and away, the very best instructor I have ever had. Very tough, but exceedingly generous with his time. And as Francis remarked, one always left his office feeling as if a fog had been blown away from an otherwise misty idea. I miss that feeling. And I will miss Peter.
This is really a sad surprise. He was truly gifted at explaining econometrics in an intuitive way, which showed his great understanding. I would look forward to getting each new edition of his Guide to Econometrics, which really kept up with the advances in the field amazingly well for such an intuitive book. My brief firsthand experience with him was in an email pointing out an error. He responded very graciously.
This is a great loss.
This is a great post on a somber topic. Peter taught me a lot while I was a grad student at SFU. He was impressive in a lot of ways. I remember his response to a student who expressed their difficulty with memorizing formulas for estimators: a good way to memorize something is to test yourself in the shower each morning – if you’ve failed to remember what you wanted you ought to give yourself a good blast of cold water. I share that, along with many of his other insights with my students regularly.
Peter was a brillient teacher, best I ever had. He set the standard for teaching to which I aspire in my own career. Additionally, he provided me with a very valuable piece of advice for a young economic theorist: if you can’t simulate it on a computer, you really don’t understand it at all. I can’t tell you how many times this saved me from embarrassment. Before his passing I looked forward to many more years of interaction with Peter, and though this will not happen in person, his legacy will live on through me and all of the others he has touched.