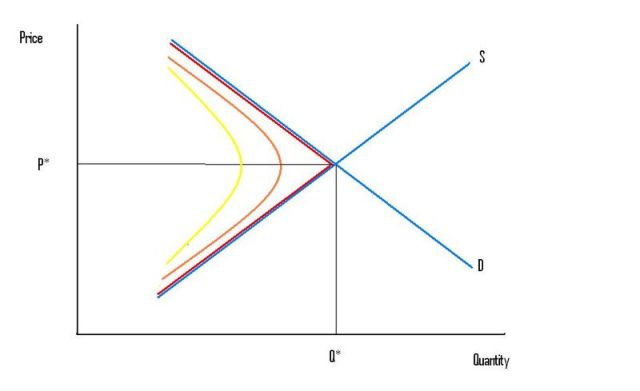
Take a simple supply and demand model of a competitive market. Look at the blue lines in my picture below:
If the price is at P*, the quantity traded will be at Q*. We are at the intersection of the two blue lines.
What happens when the price is above or below P*? We now invoke the "Short Side Rule". Quantity traded will be whichever is less: quantity demanded; or quantity supplied. Q=min{Qd,Qs}. As the price changes, relative to P*, we move along the kinked red line in the picture.
What happens when we add search into the model? Quantity traded will be some function, called a "matching function", of quantity demanded and quantity supplied. That matching function will look something like the orange curve.
If search gets harder — if it gets harder for buyers and sellers to find each other — the orange curve will shift leftward, to the yellow curve. At the same price, the same quantity demanded and supplied results in fewer buyers and sellers finding each other, and so a smaller quantity of trades. Plus, search costs are like a tax on trade, so there's less quantity demanded and supplied at any price.
If search gets easier — if it gets easier for buyers and sellers to find each other — the orange curve will shift rightwards, and get more curved. In the limit, as search costs approach zero, the matching function approaches the kinked red line.
We can think of the simple supply, demand, and Short Side Rule as simply a limiting case of a search model.
As price rises above P*, the simple model says there is an excess supply. There are sellers searching for buyers, and no buyers searching for sellers. Buying more is trivially easy; selling more is totally impossible.
A search model says there is always excess supply and excess demand, at any price. There are always sellers looking for buyers and buyers looking for sellers.
But as the price rises, the number of sellers looking for buyers increases; and the number of buyers looking for sellers decreases. So it becomes easier, but not trivially easy, for a buyer to find a seller and buy more; and harder, but not impossibly hard, for a seller to find a buyer and sell more. [Edited the last sentence for greater clarity.]
The simple Q=min{Qd,Qs} story is just a simplified, limiting case of a search model. It's not wrong. It's just a simple model. And like all models it leaves stuff out. No biggie.
So when we see that it is unusually hard for sellers to find buyers, and unusually easy for buyers to find sellers, it's quite OK to say that it looks like a market in excess supply. It's a simplification of reality. But so is all economics.
That's how I look at it, anyway.
This post is in response to Paul Krugman on Bob Hall:
"Nice point about how Ned Phelps declared, 40 years ago, that “we have made a landing on the non-Walrasian continent” and that “the days of Q= min[S(p), D(p)] are over” — when in fact, as Bob says, exactly that story — the short side determines output and employment — is exactly the way we do useful macro, even now.
…………..
So the point, as I get it, is that zero-lower-bound models work very well in practice, but have a problem in theory: it’s not at all clear how to reconcile them with Diamond-Mortenson-Pissarides-type [search] models of the labor market.
My first reaction — but I think it’s wrong — is, so much for DMP. But he’s right: we do need to figure out what’s actually going on in the labor market (although I don’t think I agree with his proposed reconciliation)."
Another masterful post. Truly, Nick, I’ve learned more economics from you than from 95% of the professors I had in my undergraduate economics degree.
Your way of explaining concepts is always clarifying and thought provoking
Awesome. Now if you could add monopolistic competition, I may start to understand 🙂 Maybe Supply and demand of all goods would be a multidimensional cube around a spherical search space.
JCE: Thanks! I really appreciate your saying that. Since being a teacher of economics is what pays my salary (admin work aside).
edeast; Thanks! Your question is exactly the same question I was asking myself, last night after I posted this. How to add degree of monopoly power, and monopolistic competition, to the same diagram. I don’t have a clear simple answer yet. It’s of course easy to do in the case of no search costs. The equilibrium under monopoly will be somewhere along the downward-sloping part of the red line, and as the degree of monopoly power gets bigger, it’s further away from the kink. (And with monopsony power, it’s on the upward-sloping bit of the red line.)
Here’s a rough sketch of answer:
Let search costs get bigger and bigger, so the yellow curve shifts leftward, until the point where it just barely kisses the vertical axis, so the market is at the point of vanishing altogether. Call that point on the vertical axis the “kiss point”. Now draw a bunch of curves radiating out from the kiss point, like a fan. Each of those “fan curves” is associated with a particular degree of monopoly/monopsony power. That particular fan curve which passes through the supply/demand equilibrium (where the blue lines cross) is where buyers and seller have equal power. That’s the competitive fan curve, where buyers and seller have equal market power. Fan curves above that have more pricing power to the seller: monopoly. Fan curves below that have more pricing power to the buyer: monopsony. Equilibrium is where a fan curve cuts one of the yellow, orange, or red curves.
On second thoughts, I’m not sure my answer to edeast’s good question is exactly right. The hinge of the fan may be broken. Monopoly of monopsony power might destroy a market, if search costs are big, that could survive under competition. (It’s not worth searching for a seller, because even if you find one he will charge too high a price, now that your search costs are sunk.) Maybe the fan curves don’t all start from the same point on the vertical axis.
Will have to think some more.
Yep. The fan curves won’t cross each other, but the hinge of the fan will be to the left of the vertical axis. Only the competitive fan curve will pass through the kiss point and end where the S and D curves intersect.
Such a pretty picture…
is the “short side rule” a standard concept in teaching basic supply and demand these days?
i don’t recall it from my days (very last century)
Thanks Frances! All because daughter #2 taught me how to use Paint.
anon: as far as I know, first year texts don’t actually use the term “short side rule” (though I use it when I teach). But they all implicitly invoke the short side rule, usually right after introducing supply and demand, when they talk about price controls. Rent controls lead to Q=Qs. Minimum wage laws lead to Q=Qd. I didn’t learn the term until PhD macro, with Peter Howitt. But when I heard him say it, I realised he was just formalising something I already knew, implicitly. It’s an implication of exchange being voluntary. You can’t force a buyer to buy, and you can’t force a seller to sell.
I wrote a follow up last night but didn’t post it cause i thought I was off base. but here it is.
If you add a z axis, the angle away from the plane of the productA that you have there, could be considered degree of differentiation between products, eg a product at 90degrees, is completely independent of A’s s/d vectors, not a substitute. If the angle is small enough, ie degree of differentiation between products A&B is not too large, and the search function of product A yellow is less then the search function for product B, in the same direction as product A then substitution for B would occur. Also I’m renaming the term quantity along the x axis as attribute, or quality, in my mind to generalize it.
I’m considering monopolistic competition, as decommodification between similar goods.
So the larger difference in angles, the greater monopoly power, less you have to worry about substitutes, in the same direction as Q. More freedom to vary S.
Ok, I’ve almost generalized it, I’m just not sure of whether goods, are vectors on state space of requirements, or if each good itself, is an axis. Ie, the platonic ideal commodity, vs the actual available commodity.
For example, your graph of a market, say is of quantity of dollars, and quantity of good A. Intersection Q* is price. I’m trying to figure, out if the P, is ideal moe, or if it is a vector of moemoaand everything else.
If we had close money substitutes, small angle difference from vertical, and they suddenly collapse, boost demand for the monopolistic good that approaches the ideal need liquidity? still not sure of how this effects supply and demand.
But at least the curves go asymptotic, eg unobtanium, from very close to the axis, supply of .01 massive demand. As long as there are no close substitutes on the ideal axis that unobtanium represents.
So in terms, of dollars P every other good within that currency domain lays along the z/q plane. and that is the price level. I’ve got to go finish finals, I wish you held off blogging another week.
also could the search curves represent, the difference that you keep mentioning between actually supplied goods, and supplied goods.
Try and merge the concepts, if the fan angled up is degree of monopoly, and we complete the drawing of the fan as a disk all the way around the P axis. The point at which the fan curve intersects the other good, should be equal to the other good’s Q*.
So when the curve passes through the z axis perpendicular where it started its value is = to the hinge. money = money no Q exchanged.
And hinge can be located on the axis, with the asymptotic nature of the demand curves, the market it there but it is bounded by the resources along P, and the availability of close vector substitutes.
The figures is very pretty, and the post is good and illuminating for me. Sadly, I can not understand well the Krugman´s text, nor his intention.
edeast: “also could the search curves represent, the difference that you keep mentioning between actually supplied goods, and supplied goods.”
In the simple supply and demand model, the blue curves represent the quantities people would like to buy and sell. The red kinked curve shows the quantities they actually buy and sell. Gneralising to the search models: with search costs, the orange (or yellow) curves now show the quantities they actually buy and sell.
For me, the best way to represents different goods of different qualities is as points in n-dimensional characteristics space. For example, if you only care about the location of a restaurant, each restaurant can be represented as a point in 2-dimensional space. A street map. And a cluster of restaurants that are close together will be closer substitutes to each other.
Luis: thanks! Paul Krugman is saying that basic macro models assume Q=min{Qs,Qd}, but the best theory uses search models. He asks how do we reconcile the two? My post is a partial answer.
Oh, ok. I agree. I´ve borrowed your graph to my post. It is the best illustration I´ve never seen on the topic.
BTW, I see that a market with an only offering and demanding labor there will be no cost of seaching. There will be ohter kind of cost, but not of searching.
Luis: I don’t understand your 6.02 comment?
Sorry, I tnink that if there is monopoly in one of both direction (demand or supply), the problem is not the cost of searching.
Ya sorry about going manic in the comments, a lot of stress, and writing as my neurons were firing. I’m done, its in my mind, but I’ll put in more work to crystallize it before I try to get it out. Thanks.
Surely your orange curve should asymptotically approach the red curve at each end, since search costs should approach zero.
I envisage it like a street of homogeneous restaurants. On a quiet day, all of the restaurants are half empty and you can go in the first one you see. On a really busy day, all the restaurants are full and crowds are milling around. It is straightforward for a waiter to pull someone in off the street (or out of a queue) as soon as they have a vacant table. On an equilibrium day, most restaurants are full and the streets are fairly quiet. You need to go up and down the street looking for an empty table.
Ok, I drew a picture to explain my previous comments.
edeast: no worries! enthusiasm is good. I don’t really understand your pictures though. I will have another go later. It’s still early here.
Luis: OK. Agreed. Monopoly/monopsony, and search costs, are two separate problems. Each can make the quantity traded smaller than it would otherwise be. But there’s an interaction. Even if there’s a large number of small identical buyers and sellers, once a buyer meets a seller both sides would face the costs of searching for a substitute if they can’t agree on a price. So there’s ex-post bilateral monopoly/monopsony.
Dave: I was trying to draw the orange curve to asymptote the red curve at each end. It’s a plausible assumption, under some conditions. But it doesn’t have to be like that. Even if all restaurants have empty seats, it might take 10 minutes to walk to the nearest restaurant. So there will be a minimum 10 minute gap between the orange and red curves. It depends on the density of buyers an sellers. A thick or thin market.
The orange curve could also be asymmetric. Think about fire engines. At most times, there are more unemployed fire engines (waiting for a fire) than there are vacancies (fires waiting for a fire engine). It’s better that way, because the cost of an unemployed fire engine is less than a vacancy.
Quote: “This post is in response to Paul Krugman on Bob Hall:….”
A-ha! So, you are talking of the labour market with that single commodity model? I didn’t recognise it until I read the quoted part.
You are in a pitfall. In case of labour market the demand curve must be upward sloping though less steep than the supply curve. The idea is:
1. Quantity is volume of labour.
2. Price is not the average wage but the yield of the economy.
The demand curve represents the (expected) production as a function of volume of labour, which is identical with the aggregate demand. The supply curve represents a function of volume of labour, which is identical with the aggregate supply. Then, the point of intersection indicates the effective demand and the corresponding volume of labour.
Meantime, the ‘mainstream’ (i.e. neoclassical) economists (and probably the Austrian-school economists) assume that the schedule of investment is identical with the schedule of saving. Therefore;
I = Y – C (I: investment, Y: aggregate income, C: consumption)
As the aggregate demand (D) is the sum of consumption and investment:
D = C + I = C + (Y – C) = Y
As aggregate supply (Z) is the same as aggregate income:
Z = Y
Therefore:
D = Z
This means that the mainstream economists (and probably the Austrian economists) are thinking that the demand curve and the supply curve are identical with each other. That’s why the graph looks meaningless to them if you draw it according to 1 and 2.
On the other hand, you may introduce propensity to consume and think of consumption as a function of volume of labour (n):
C = X(n)
Aggregate income of enterprises is aggregate demand (D). It can be divided into spending for consumption (Dc) and spending for investment (Di):
D = Dc + Di
Actual volume of labour depends on D. As the demand curve is described as a function of volume of labour (F(n)):
D = F(n)
If aggregate supply is f(n), effective demand is decided as:
F(n) = f(n)
Therefore;
f(n) = X(n) + Di
As volume of labour increases X(n) increases less steep than f(n), because propensity to consume is between 0 and 1. If Di doesn’t grow quick enough to fill the gap, aggregate supply becomes correspondingly excessive. This means the supply curve is steeper than the demand curve as I said above.
The ‘Short Side Rule’ is applied there, too, as a matter of course. In this case, the red, orange and yellow lines look fairly different. Try and draw the graph for yourself.
(A megaquake-style aftershock occurred while I was reading your entry. Scary. I will be reluctant to read your entry).
Jasiek:
You are waaaay off topic here. Not everything can be forced onto the procrustean bed of the General Theory. (Yes, I have read it, by the way).
Assume L=Y and P=W just for simplicity (output is backscratches, so employment is output, and the wage is the price). What you have just described is the Keynesian Cross model. What you are calling the “labour demand curve” is what we normally call the AE curve. What you are calling the “labour supply curve” is the 45 degree semi-equilibrium condition. And, it’s not in any way a labour supply curve. “Supply means what you would like to sell, not what you actually sell. That Keynesian Cross model is talking about the downward-sloping part of the red line in my model. Except it has a totally different vertical axis. It’s L=min{Ld,Ls}, under the assumption that Ls exceeds Ld, and where Ld itself is a function of L.
Here’s my old post on the Keynesian Cross: http://worthwhile.typepad.com/worthwhile_canadian_initi/2011/01/understanding-the-keynesian-cross.html
Do take care in Japan. I hope that tsunami doesn’t amount to anything like the last one!
trivial, trivial,
of course, the search is going on, but on different markezs. Nver on the same market! Omly an attempt to throw out classical theory. Too much confusion !
Rainer Zirbs from Germany
Mr Rowe,
Quote: “You are waaaay off topic here.”
O, am I? Weren’t you talking of the labour market by the graph? Supply of labour and demand for labour by scale of wages?
The labour demand curve? The labour supply curve? I didn’t say such things! The curves in my previous post are aggregate demand and aggregate supply curve as functions of volume of labour respectively.
Assuming Q=L (by hours) and P=Y, I am not talking about the Keynesian Cross in any way. Please re-read my post a bit more carefully. (I wonder what made you think of the graph as the Keynesian Cross. Is it because both lines are upward-sloping? Because you assume Say’s law in a broad sense?)
By the way, the Keynesian Cross model seems to be assuming:
1. Malleability, or perfect competition (You may add ‘semi-’)
2. Abundance of all scarce resources concerned
Naturally, you’d think of it as ‘weird’ and ‘strange’. The semi-equilibrium conditions, therefore, can be both valid and non-valid depending on the timespan you consider in this real world, as it may maintain some validity with what you call a single-commodity model. Thus, the model’s another pitfall.
Turning to your graph, if it’s about the labour market (P=W/P, Q=N), the demand line means the first postulate of the ‘mainstream’ economics is fulfilled and the supply line means the second postulate is fulfilled. Thus, a pitfall, I say. That may lead to a Wal-Mart economy.
The linked entry is very interesting in general but the explanation of ‘stairs’ in there doesn’t sound convincing to me. With the extra income I’d buy a share in Apple Inc. instead, and thus the economy eventually suffers a less propensity to consume. Whether an enterprise increases investment into production depends on its long-term expectation. That’s how the quantity theory of money doesn’t work. (Regarding barter economy, please re-read Chapter 17-V of the General Theory, where he is talking of a ‘non-monetary’ economy and its conditions).
Tsunami is the biggest concern here indeed. The locals have already evacuated, but the naughty GE reactors, which the guys there are trying to tame, can’t. That’s why scary. Imagine the vessels would pop and splash plutonium high in the sky. Luckily, only little props of seawater were observable last night.
The biggest challenge is, however, not the reactors but the public finances and economic growth here. I posted the three-stage method to your previous entry, and I believe that’d work under the current conditions, which Paul Krugman may regard as a (semi-)liquidity-trap. The key is political consensus for progressive taxation. O, I’ve gone off topic. Excuse me. And, I know you’ll assume a critical attitude towards my idea.
You’d better go back to the General Theory from time to time. It’s such a rough sketch by Keynes and his ‘circus’ that it doesn’t meticulously explain everything as a matter of course. But, in it he introduced extremely important notions, some of which have long been overlooked. Why do you stick to equilibrium analysis that much?
Regards,
Jasiek
According to Keynes’ dichotomy between household and enterprise, if you think of the macroeconomic conditions things would look a bit different from the microeconomic conditions:
1. A monopolistic economy means there’s only one supplier (of all the goods and services)
2. A monopsonic economy means there’s only one buyer (of all the goods and services)
Then;
1. In a monopolistic economy the enterprises collectively sell goods and services, and thus it’s equal to a one-company economy.
2. In a monopsonic economy the households collectively buy goods and services, and distribute them among themselves somehow efficiently.
Otyn Harasho. We should avoid fallacy of composition.
On the other hand, the mainstream economics assume that an economy is divided into independent individuals. That’s the source of fallacy of composition.